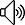Empiricial Risk Minimization

統計學習理論是整個機器學習到框架。試想我們學習的目的是什么呢？當然是為了具備用合理的方式處理問題的能力。統計學習理論要解決的問題就是基于數據找到一個預測函數。經驗風險最小化(Empiricial Risk Minimization,ERM)[2]是統計學習理論中準則之一，常用于給出學習算法(learning algorithms)性能的理論邊界。 假定給定兩個數據空間\(X\)和\(Y\), 我們想學習到一個假設函數(hypothesis function)\(h:X\rightarrow Y\)。對于任意的\(x\in X\), 我們可用假設函數求得\(x\)在空間\(Y\)中對應的映射\(y\in Y\)，即\(y=h(x)\)。假設\(X\)和\(Y\)之間存在聯合概率分布\(P(x,y)\)，注意在聯合概率的假設下，\(x\)和\(y\)之間不存在單一映射關系。具體而言，即使給定\(x\)，\(y\)依然是個隨機變量，最合理的\(y\)就是使不確定性最小的：\(y=arg\underset{y\in Y}{\max}\;P(y|x)\)。如何衡量我們預測的結果好不好呢？損失函數(loss function)登場了，損失函數\(L(y,\hat{y})\)度量預測值\(\hat{y}\)與真實值\(y\)之間的差距，兩者越相近，對應的損失也就越小。在二分類問題中，損失函數常定義為\(L(y,\hat{y})=I(y\neq\hat{y})\)；在回歸問題中，損失函數更傾向于\(L(y,\hat{y})=(y-\hat{y})^2\)。假設函數\(h(x)\)的風險(泛化誤差)定義為損失函數的期望： \begin{equation} R(h)=\mathbb{E}\left[L(h(x),y)\right]=\int L(h(x),y)d P(x,y) \end{equation} 學習算法的終極目標是在假設集合\(\mathcal{H}\)中找到最優的假設函數\(h^{\star}\)，使得風險\(R(h)\)最?。?\begin{equation} h^{\star}=arg \underset{h\in\mathcal{H}}{\min}\;R(h) \end{equation} 絕大多數情形下，我們不知道概率分布\(P(x,y)\)，使得學習算法無法計算\(R(h)\)。但是我們可以通過在\(P(x,y)\)上采樣的方式來計算\(R(h)\)的近似值。假設我們從\(P(x,y)\)采樣得到的\(m\)個獨立同分布的樣本組成訓練集\(\mathcal{S}=\{(x^{(i)},y^{(i)})\}_{i=1}^m\)，那么風險\(R(h)\)對應的近似值\(\hat{R}(h)\)只需在訓練集上計算損失函數的均值即可： \begin{equation} \hat{R}(h)=\frac{1}{m}\sum_{i=1}^mL(h(x^{(i)},y^{(i)}) \end{equation} 其中\(\hat{R}(h)\)即為經驗風險(empirical risk)。經驗風險最小化準則闡述的規律就是使經驗風險最小的假設函數對應實際的最優假設函數\(h^{\star}\)的近似值\(\hat{h}^{\star}\): \begin{equation} \hat{h}^{\star}=arg\underset{h\in\mathcal{H}}{\min}\;\hat{R}(h) \end{equation} 根據大數定理可知，在訓練數據足夠多的情況下(\(n\rightarrow\infty\))，經驗風險是可以收斂到真實的泛化誤差的。但在大多實際應用中，可用于訓練模型的樣本卻往往非常有限。因此，在有限的訓練數據情形下，使經驗風險最小的假設函數，其對應的泛化誤差不一定是最小的，即可能不是泛化能力最強的假設函數，如圖1所示。?

Probabilistic Inequalities

在展開學習理論之前，非常有必要簡單回顧并證明一下相關的概率不等式，這是進一步討論學習理論的基礎。

定理一(Jensen's Inequality)[4]

假設\(X\)為隨機變量，\(f:X\rightarrow\mathbb{R}\)為凸函數(convex)，有 \begin{equation} f\left(\mathbb{E}[X]\right)\leq \mathbb{E}\left[f(x)\right] \end{equation} 如果\(f\)為凹函數(concave)則有相反的結論 \begin{equation} f\left(\mathbb{E}[X]\right)\geq \mathbb{E}\left[f(x)\right] \end{equation}

定理二(Markov's Inequality)[5]

假設\(X\)為非負的隨機變量，對任意的\(t>0\)，有 \begin{equation} P(X>t)\leq\frac{\mathbb{E}[X]}{t} \end{equation}

證明： \begin{equation} \begin{array}{rl} \mathbb{E}[X]&=\int_{0}^{+\infty}xp(x)dx=\int_{0}^{t}xp(x)dx+\int_{t}^{+\infty}xp(x)dx\\ &\geq \int_{t}^{+\infty}xp(x)dx \geq t\int_{t}^{+\infty}p(x)dx=tP(X>t) \end{array} \end{equation}

定理三(Chernoff Bound)[1]

假設\(X\)為隨機變量,有 \begin{equation} P(X>\epsilon)\leq\underset{t\geq 0}{\inf}\exp(-t\epsilon)\mathbb{E}[\exp(tX)] \end{equation} 其中\(inf\)表示函數的最大下界。

證明： \begin{equation} \begin{array}{rl} P(X>\epsilon)&=P\left(\exp(X)>\exp(\epsilon)\right)\\ &=\underbrace{P\left(\exp(tX)>\exp(t\epsilon)\right)\leq\exp(-t\epsilon)\mathbb{E}[\exp(tX)]}_{Markov's \; inequality} \end{array} \end{equation}

定理四

假設隨機變量\(X\in[a,b]\)，\(\mathbb{E}[X]=0\)，有 \begin{equation} \mathbb{E}[\exp(tX)]\leq\exp\left(\frac{t^2(b-a)^2}{8}\right) \end{equation}

證明： 在\(a\neq 0,b\neq 0\)時，我們可以將\(X\)表示成\(a\)和\(b\)的線性組合\(X=\alpha b+(1-\alpha)a\)，其中\(\alpha=(X-a)/(b-a)\in[0,1]\)。對于凸函數\(f(x)=\exp(tx)\)，如果我們將\(X\)視為一個Bernoulli分布的隨機變量(即\(P(X=b)=\alpha,P(X=a)=1-\alpha\))，那么根據Jensen不等式，有 \begin{equation} f(X)=f(\alpha x+(1-\alpha)b)\leq\alpha f(x)+(1-\alpha)f(b) \end{equation} 將\(X=\alpha b+(1-\alpha)a\)帶入上述不等式中，得 \begin{equation} \exp(tX)\leq\frac{X-a}{b-a}\exp(tb)+\frac{b-X}{b-a}\exp(ta) \end{equation} 在上式左右兩邊求期望值，結合\(\mathbb{E}[X]=0\)，有 \begin{equation} \mathbb{E}[\exp(tX)]\leq-\frac{a}{b-a}\exp(tb)+\frac{b-a}\exp(ta)=\exp(g(u)) \end{equation} 其中\(u=t(b-a)\),\(g(u)=-\theta u+\log(1-\theta+\theta\exp(u))\),\(\theta=-a/(b-a)\in(0,1)\)。 根據二階Taylor展開公式，存在\(v\in(0,u)\)使得下式成立： \begin{equation} g(u)=g(0)+ug'(0)+\frac{u^2}{2}g''(v) \end{equation} 接下來，對\(g(u)\)求一階倒數和二階倒數 \begin{equation} g'(0)=-\theta+\frac{\theta\exp(u)}{1-\theta+\theta\exp(u)}\vert_{u=0}=0 \end{equation} \begin{equation} g''(v)=\frac{\theta\exp(v)}{1-\theta+\theta\exp(v)}\left(1-\frac{\theta\exp(v)}{1-\theta+\theta\exp(v)}\right)\leq\frac{1}{4} \end{equation} 該不等式成立，因為對任意\(s\in[0,1]\)，有函數\(s(1-s)\leq\frac{1}{4}\)。將\(g(0)=0\),\(g'(0)=0\),\(g''(v)\leq 1/4\)和\(u\)帶入Taylor展開式中，得到以下不等式： \begin{equation} g(u)=\frac{u^2}{2}g''(v)\leq\frac{u^2}{8}=\frac{t^2(b-a)^2}{8} \end{equation} 由上式可得 \begin{equation} \mathbb{E}[\exp(tX)]\leq\exp\left(\frac{t^2(b-a)^2}{8}\right) \end{equation} 我們可以驗證，在\(a=b=0\)時，上述不等式仍然是成立的。

定理五(Hoeffding's Inequality)[3]

假設\(X_1,\cdots,X_n\)為\(n\)個相互獨立的隨機變量,且\(X_i\in[a_i,b_i]\)，\(\bar{X}=\sum_{i=1}^nX_i/n\)，則對任意的\(\epsilon>0\)有 \begin{equation} P\left(|\bar{X}-\mathbb{E}[\bar{X}]|>\epsilon\right)\leq 2\exp\left(\frac{2n^2\epsilon^2}{\sum_{i=1}^n(b_i-a_i)^2}\right) \end{equation}

證明：根據對稱性、Chernoff邊界定理、定理四以及隨機變量間的相互獨立性質，可推導出下式 \begin{equation} \begin{array}{rl} &P\left(|\bar{X}-\mathbb{E}[\bar{X}]|>\epsilon\right)\\ =&2P\left(\bar{X}-\mathbb{E}[\bar{X}]>\epsilon\right)\\ \leq& 2\underset{t\geq 0}{\inf}\exp(-t\epsilon)\mathbb{E}[\exp(t\bar{X})]\\ =& 2\underset{t\geq 0}{\inf}\exp(-t\epsilon)\mathbb{E}[\exp(t\sum_{i=1}^nX_i/n)]\\ =& 2\underset{t\geq 0}{\inf}\exp(-t\epsilon)\mathbb{E}[\prod_{i=1}^n\exp(tX_i/n)]\\ =& 2\underset{t\geq 0}{\inf}\exp(-t\epsilon)\prod_{i=1}^n\mathbb{E}[\exp(tX_i/n)]\\ \leq & 2\underset{t\geq 0}{\inf}\exp(-t\epsilon)\prod_{i=1}^n\exp(t^2(b_i-a_i)^2/(8n^2))\\ =& 2\underset{t\geq 0}{\inf}\exp(-t\epsilon+\sum_{i=1}^nt^2(b_i-a_i)^2/(8n^2)) \end{array} \end{equation} 為了得到盡可能接近真實值的上階，我們還剩最后一步，即求出上式最右側函數的最大下界。定義函數\(p:\mathbb{R}\rightarrow\mathbb{R}\)為 \begin{equation} p(t)=-t\epsilon+\sum_{i=1}^n\frac{t^2(b_i-a_i)^2}{8n^2} \end{equation} 很顯然\(p(t)\)是一個二次函數，其最大下界可在極值點出取得： \begin{equation} p'(t)=-\epsilon+\frac{t\sum_{i=1}^n(b_i-a_i)^2}{4n^2}=0 \end{equation} 解上式可得 \begin{equation} t=\frac{4n^2\epsilon}{\sum_{i=1}^n(b_i-a_i)^2} \end{equation} 將\(t\)帶入\(p(t)\)即可得Hoeffding不等式： \begin{equation} P\left(|\bar{X}-\mathbb{E}[\bar{X}]|>\epsilon\right)\leq 2\exp\left(-\frac{2n^2\epsilon^2}{\sum_{i=1}^n(b_i-a_i)^2}\right) \end{equation}

定理六(Union Bound)[8]

對于有限個事件\(A_1,A_2,\cdots,A_n\)，有 \begin{equation} P\left(\bigcup_{i=1}^nA_i\right)\leq\sum_{i=1}^nP(A_i) \end{equation}

證明： 我們用歸納法來證明該定理。在\(n=1\)時，顯然\(P(A_1)\leq P(A_1)\)；假設在\(n=k\)時，\(P\left(\bigcup_i^kA_i\right)\leq\sum_{i=1}^nP(A_i)\)成立；那么在\(n=k+1\)時，結合\(P(A\cup B)=P(A)+P(B)-P(A\cap B)\)，有 \begin{equation} \begin{array}{rl} P\left(\bigcup_{i=1}^{k+1}A_i\right)&=P\left(\bigcup_{i=1}^{k}A_i\right)+P(A_{k+1})-P\left(\bigcup_{i=1}^{k}A_i\cap A_{k+1}\right)\\ &\leq\sum_{i=1}^kP(A_i)+P(A_{k+1})=\sum_{i=1}^{k+1}P(A_i) \end{array} \end{equation} 綜上所述，可知該定理成立。

Model complexity and Generalization Error

機器學習求解的假設函數不是單純為了擬合已有的數據，其最終目標是準確預測未知數據的輸出。經驗風險最小化存在過擬合的風險，其目的在于找到一個可以很好與訓練數據匹配的假設函數，而該假設函數不一定能預測未知數據的輸出。如圖2所示，訓練數據的規模\(m\)、模型復雜度和泛化誤差\(R(h)\)三者間存在一定的關系。我們如何避免過擬合？我們可以從兩方面應對這個問題。 從圖2(a)中可知，增加訓練數據的規模有利于降低泛化誤差。但也不是訓練數據越多越好，因為當訓練數據達到一定規模后，泛化誤差的變化趨于平緩。那么一定的規模到底是個什么概念呢？這對應我們后面即將說明的算法的樣本復雜度。觀察圖2(b)，可知模型復雜度太大或者太小都會導致泛化誤差過大。因此，另一個避免模型過擬合的方法就是控制模型復雜度。 機器學習領域有個警句，"Sometimes it's not who has the best algorithm that wins;it's who has the most data"?，F在大數據也吵得火熱，圖2也可以幫助我們理解為什么大量的訓練數據加上一般的模型產生的威力可能要強于少量的訓練數據加上優秀的模型。但是呢，縱然現在有分布式計算作為支撐，過多的訓練數據還是會帶來很大的存儲、通信和計算開銷，但在有些情形下盲目增大訓練數據的規模意義不大；另一方面，在某些領域想要獲取足夠多的訓練數據不是那么容易的。在研究機器學習算法時，模型的復雜度是我們更為關心的問題。

The case of finite \(\mathcal{H}\)

我們用\(|\mathcal{H}|\)表示假設集合\(\mathcal{H}\)中包含的假設函數的數目，有限個假設函數組成假設集合\(\mathcal{H}=\{h_1,h_2,\cdots,h_{|\mathcal{H}|}\}\)，根據經驗風險最小化的原則，從假設集合\(\mathcal{H}\)中估計出的最優假設函數滿足訓練誤差最小的條件： \begin{equation} \hat{h}=arg\underset{h_i\in\mathcal{H}}{\min}\hat{R}(h_i) \end{equation} 下面要證明的是使訓練誤差較小的假設函數\(\hat{h}\)，其泛化誤差也不至于太大。我們分兩步完成這個證明：首先，對任意假設函數\(h\)而言，\(\hat{R}(h)\)都是\(R(h)\)的一個可靠的近似值；其次，給出\(\hat{h}\)的泛化誤差\(R(\hat{h})\)的上界。 我們在樣本空間內根據樣本的概率分布\(\mathcal{D}\)進行采樣，得到訓練集\(\mathcal{S}=\{(x^{(i)},y^{(i)})\}_{i=1}^m\)。給定任意假設函數\(h_i\in\mathcal{H}\)，定義服從Bernoulli分布的隨機變量\(Z_j=I\{h_i(x^{(j)})\neq y^{(j)}\}\in\{0,1\}\)，則\(Z_j\)表示\(h_i\)是否將樣本\((x^{(j)},y^{(j)})\)誤分類了，\(h_i\)的泛化誤差\(R(h_i)=P(z_j=1)\)。因為所有樣本都是從同一個概率分布中獨立采樣的，所以\(\{Z_j\}_{j=1}^m\)中的都是滿足獨立同分布的Bernoulli隨機變量。\(h_i\)的訓練誤差形式為： \begin{equation} \hat{R}(h_i)=\frac{1}{m}\sum_{j=1}^mI\{h_i(x^{(j)})\neq y^{(j)}\}=\frac{1}{m}\sum_{j=1}^mz_j \end{equation} 顯然\(\hat{R}(h_i)\)為\(m\)個獨立同分布的Bernoulli隨機變量的均值，且這些隨機變量的期望值都為\(R(h_i)\)。根據Hoeffding不等式，得到如下規律： \begin{equation} P\left(|R(h_i)-\hat{R}(h_i)|>\gamma\right)\leq 2\exp(-2\gamma^2m) \end{equation} 上述規律說明：對特定假設函數\(h_i\)而言，在樣本數目\(m\)足夠大時，訓練誤差和泛化誤差近似相等的概率可以非常大，這也證明了\(\hat{R}(h)\)都是\(R(h)\)的一個可靠的近似值。 但我們想要保證的不僅僅是這種近似的可靠性只對特定的假設函數成立，而是對假設集合\(\mathcal{H}\)中的所有假設函數都成立?，F將事件\(A_i\)定義為\(|R(h_i)-\hat{R}(h_i)|>\gamma\)，則由上一個結論可得\(P(A_i)\leq 2\exp(-2\gamma^2m)\)。 \begin{equation} \begin{array}{rl} &P\left(\exists h\in\mathcal{H}.|R(h_i)-\hat{R}(h_i)|>\gamma\right)\\ =&P(\bigcup_{i=1}^{|\mathcal{H}|}A_i)\\ \leq & \sum_{i=1}^{|\mathcal{H}|}P(A_i)\\ \leq & 2\sum_{i=1}^{|\mathcal{H}|}\exp(-2\gamma^2m)\\ =& 2|\mathcal{H}|\exp(-2\gamma^2m) \end{array} \end{equation} 上述事件的對立事件對應的概率為： \begin{equation} \begin{array}{rl} &P\left(\neg\exists h\in\mathcal{H}.|R(h_i)-\hat{R}(h_i)|>\gamma\right)\\ =&P\left(\forall h\in\mathcal{H}.|R(h_i)-\hat{R}(h_i)|\leq\gamma\right)\\ \geq & 1-2|\mathcal{H}|\exp(-2\gamma^2m) \end{array} \end{equation} 上式被成為一致性收斂(uniform convergence)，因為這個邊界值對\(\mathcal{H}\)中的所有假設函數都成立。由此可知，\(\mathcal{H}\)中的所有假設函數的訓練誤差與泛化誤差偏離范圍在\(\gamma\)以內的概率至少為\(1-2|\mathcal{H}|\exp(-2\gamma^2m)\)。 現在，我們已經得到了訓練樣本數目\(m\)、訓練誤差與泛化誤差間的偏離上限\(\gamma\)及其發生最大偏差時的的概率下限\(1-2|\mathcal{H}|\exp(-2\gamma^2m)\)三者間的關系，在給定其中兩個值的情況下我們可以推出第三個變量需要滿足的條件。比如說，為了確保所有假設函數的訓練誤差和泛化誤差間的偏差范圍都在\(\gamma\)以內的概率至少為\(1-\delta\)，至少需要多少個訓練樣本？這個問題對應的數學表述為： \begin{equation} P\left(\forall h\in\mathcal{H}.|R(h_j)-\hat{R}(h_j)|\leq\gamma\right)\geq 1-2|\mathcal{H}|\exp(-2\gamma^2m)\geq 1-\delta \end{equation} 求解上述不等式，可得訓練樣本數目\(m\)的下界： \begin{equation} m\geq\frac{1}{2\gamma^2}\log\frac{2|\mathcal{H}|}{\delta}=O\left(\frac{1}{\gamma^2}\log\frac{|\mathcal{H}|}{\delta}\right) \end{equation} 這條規律對我們是非常有用的，由此我們可以推測算法性能要達到某種水平，至少需要多少個樣本就足夠了，這也稱為算法的樣本復雜度(sample complexity)。一般而言，\(\log |\mathcal{H}|\)增長很慢，據CMU的Andrew Moore所說，\(\log |\mathcal{H}|\leq 30\)。樣本數目太少不能保證訓練出來的模型有較優的性能，樣本數目也沒必要太多太多，尤其在樣本的收集比較困難的情況下，只要能在模型性能達到期望的效果，樣本越少越好。 同樣地，假設樣本數目\(m\)和\(\delta\)都確定了，我們想知道假設集合\(\mathcal{H}\)中所有假設函數的訓練誤差和泛化誤差間偏離程度\(\gamma\)： \begin{equation} |R(h_j)-\hat{R}(h_j)|\leq\gamma\leq\sqrt{\frac{1}{2m}\log\frac{2|\mathcal{H}|}{\delta}} \end{equation} 接下來，我們即將給出\(\hat{h}\)的泛化誤差上界。定義假設集合\(\mathcal{H}\)中的最優假設函數為： \begin{equation} h^{\star}=arg\underset{h\in\mathcal{H}}{\min}\;R(h) \end{equation} 由于\(h^{\star}\)訓練誤差小于\(\hat{h}\)，結合\(|R(h)-\hat{R}{h}|\leq\gamma\)，可得到\(\hat{h}\)的泛化誤差上界： \begin{equation} R(\hat{h})\leq\hat{R}(\hat{h})+\gamma\leq\hat{R}(h^{\star})+\gamma\leq R(h^{\star})+2\gamma \end{equation} 上式說明，訓練誤差最小的假設函數\(\hat{h}\)的泛化誤差頂多比假設集合中最優的假設函數\(h^{\star}\)高\(2\gamma\)，即： \begin{equation} R(\hat{h})\leq\left(\underset{h\in\mathcal{H}}{\min}\;R(h)\right)+2\sqrt{\frac{1}{2m}\log\frac{2|\mathcal{H}|}{\delta}} \end{equation} 如果擴大模型的復雜度，即假設空間增大為\(\mathcal{H}'\supset\mathcal{H}\)。在\(\mathcal{H}'\)中，我們可能找到泛化誤差更小的假設函數，因此第一項不可能增大；\(\mathcal{H}'\)中假設函數的數目\(k\)增大，必然使得第二項增大。 根據如下關系： \begin{equation} R(\hat{h})\leq \hat{R}(\hat{h})+\sqrt{\frac{1}{2m}\log\frac{2|\mathcal{H}|}{\delta}} \end{equation} 我們可以總結出如下規律：在\(|\mathcal{H}|\)有限的情況下，只要樣本數目\(m\)足夠大，就有\(R(\hat{h})\approx \hat{R}(h)\)；此時若有\(\hat{R}(\hat{h})\approx 0\)，必然有\(R(\hat{h})\approx 0\)，即通過經驗風險最小化得到的最優假設函數是可靠的。但實際情況并非如此簡單：如果\(|\mathcal{H}|\)有限，在大多數情況下我們無法保證從\(\mathcal{H}\)中選擇出來的假設函數的經驗風險趨近于0(少數時候可以碰巧找到經驗風險為0的假設函數)，此時\(\hat{h}\)的泛化誤差可能無法令人滿意；如果\(|\mathcal{H}|\)趨于無限，我們雖可以保證\(\hat{R}(\hat{h})\approx 0\)，但根據上式又無法得到\(R(\hat{h})\approx \hat{R}(h)\)，使得無法確保\(\hat{h}\)的泛化誤差足夠小。在\(|\mathcal{H}|\)趨于無限時，是否真的無法保證\(R(\hat{h})\approx \hat{R}(h)\)呢？請看下面\(|\mathcal{H}|=\infty\)的情況。

The case of infinite \(\mathcal{H}\)

為什么前面推導出的\(R(\hat{h})\)的泛化誤差的上界在\(|\mathcal{H}|=\infty\)時沒多少用呢？因為在推導過錯中用到了union bound的性質，而且union bound定理中給出的上界是在假設所有假設函數\(h_i\)之間都相互獨立的前提下給出的。在實際情況中，\(\mathcal{H}\)有不少假設函數都是相似的。任意相似的兩個假設函數\(h_i\approx h_j\)，兩者有很多地方都是重疊的，也就說\(\hat{R}(h_i)=\hat{R}(h_j)\)的概率很大。顯然，\(h_i\)和\(h_j\)不可能相互獨立，此時還用相互獨立的假設計算union bound會把重疊部分重復計算多次，致使給出的上界太過松弛。舉個簡單的例子，假設\(\mathcal{H}\)為二維平面上所有直線的集合，顯然\(|\mathcal{H}|=\infty\)。如圖3中的\(x_i\)看來，二維平面中所有假設直線只有兩種，在\(x_1\)上面或下面的直線。

既然如此，我們能否找到一種策略，將所有相似的假設函數歸為有限的若干組呢？為了說明這個問題，下面我們簡要介紹VC維。

VC Dimension

VC維(Vapnik-Chervonenkis dimension)[9]用于度量分類算法的復雜度。介紹VC維之前，先引入shatter(分散)這個概念。給定\(n\)個數據組成的集合\(\mathcal{X}=\{x^{(1)},x^{(2)},\cdots,x^{(d)}\}\)，若對任意的標簽集合\(\mathcal{Y}=\{y^{(1)},y^{(2)},\cdots,y^{(d)}\}\)，都存在假設函數\(h\in\mathcal{H}\)可以完全正確分類，即\(h(x^{(i)})=y^{(i)}\)對\(\mathcal{X}\)中的所有數據都成立，則稱\(\mathcal{H}\)可以分散\(\mathcal{X}\)。假設集合\(\mathcal{H}\)的VC維\(VC(\mathcal{H})\)定義為\(\mathcal{H}\)可以分散的集合的能包含的數據的最大數目；若\(\mathcal{H}\)足以分散任意大的集合，則\(VC(\mathcal{H})=\infty\)。需要注意的是，為了證明\(VC(\mathcal{H})\)至少為\(d\)，我們只需要找到一個包含\(d\)個數據的集合能被\(\mathcal{H}\)分散即可；為了證明\(VC(\mathcal{H})\)最多為\(d\)，我們要證明不存在包含\(d+1\)個數據的集合能被\(\mathcal{H}\)分散。 為了更為直觀解釋VC維的概念，我們以只包含線性分類器(即感知機，Perceptron)的\(\mathcal{H}\)在二維平面中的情況為例進行說明。在圖4中，無論三個數據的標簽如何變化，總能找到線性分類器實現無誤差的分類。但在圖5中，三點共線，線性分類器無法完全正確處理任意的分類任務。除此之外，對于包含至少4個數據的集合，再也無法在\(\mathcal{H}\)中找到可以完美分類的線性分類器。由此可見，\(\mathcal{H}\)能分散的集合最多只能包含三個數據，因此\(VC(\mathcal{H})=3\)。實際上，在\(d\)維空間里，線性分類器的VC維是\(d+1\)?？吹竭@里，我們可能會非常氣憤，好不容易抽出時間學習VC維，竟然被告知\(d\)維空間中的線性分類器頂多可以完全正確對\(d+1\)個數據正確分類，要它有何用？值得慶幸的是，現實世界的變化還是趨于平滑的，相鄰的數據大多時候都屬于相同類別，并不需要處理所有數據都是任意類別的情形。所以即使是VC維較小的分類器也是有用武之地的。?

? ?

在統計學習理論中，VC維可用于給出分類模型的泛化誤差的概率性的上界，并且該上界獨立于樣本的分布情況。如果分類模型集合\(\mathcal{H}\)對應的VC維為\(d\)，以經驗風險最小化為最優準則，經過\(m\)個服從獨立同分布的數據訓練后得到分類模型的\(\hat{h}\in\mathcal{H}\)，\(\hat{h}\)的訓練誤差和泛化誤差間的關系為： \begin{equation} P\left(R(\hat{h})\leq \hat{R}(\hat{h})+\sqrt{\fracbr5n5555bvll{m}\left(\log\frac{2m}br5n5555bvll+1\right)+\frac{1}{m}\log\frac{4}{\delta}}\right)\geq 1-\delta \end{equation} 其中，帶根號的那一項我們在此稱之為VC置信度(也可視為模型復雜度對應的懲罰項)。具體的證明過程本想親自推導一遍的，只是看了Vapnik的大作后頓時有了力不從心的感覺，目前肯起來太吃力，所有有興趣的人士請參見[12,13]。 VC維可被有效應用于為線性分類器的泛化誤差確定一個上界，SVM就是一個成功的應用典范。但其他場合下也許行不通，我們可以用以下三中情形來簡單說明：

• 對于諸如神經網絡等非線性模型，無法較為準確估計對應的VC維；
• 對于KNN(k=1)和采用高斯核函數的SVM模型等，VC維是無窮的；
• 上界有時不能提供任何指導意義，比如分類錯誤率的上界大于1時。

假設函數的VC維越大，表明其模型越復雜，對應的表達能力也越強！復雜模型的經驗風險很小，同時也會因過于復雜帶來較大的懲罰成分。如果最后泛化誤差的上界增大，意味著泛化誤差很小的概率越來越小，模型不穩定的幾率會大大增加。奧卡姆剃刀（Occam's razor）原理提倡在多個具有處于競爭地位的可得出相同結論的理論中選擇最簡單的那個。換到我們這個語境中，可以理解成，在經驗風險最小的若干個假設函數中，優先選擇復雜度最低的模型。順帶提一下，為什么SVM要選擇間隔最大的超平面？其實這背后也是和VC維有關系的。如圖6所示，在\(n\)維空間里，如果所有數據點都可用一個半徑至少為\(R\)的球面包圍，超平面間的幾何間隔為\(2M\)，那么SVM的VC維的上界為[12]： \begin{equation} VC(\mathcal{H})\leq\min\left\lbrace\lceil\frac{R^2}{M^2},n\rceil\right\rbrace+1 \end{equation} 由上式可知，最大化幾何間隔實際上實在降低SVM的VC維；此外，對線性可分的數據而言，這些超平面對應的經驗風險為0，所以最大化幾何間隔也是在直接降低泛化誤差的上界。我以前經常在想，SVM的泛化性能和支持向量的數目是否有關系呢？這次我終于得到答案了。如果我們用留一法對SVM進行交叉驗證，那么還有一個實際風險的上界[10]： \begin{equation} \mathbb{E}[P(error)]\leq\frac{\mathbb{E}[Number\;of\;support\;vectors]}{Number\;of\;training\;samples} \end{equation} 其中\(\mathbb{E}[P(error)]\)是在\(m-1\)個樣本上訓練后用剩下的一個樣本測試得到的風險期望，\(\mathbb{E}[Number\;of\;support\;vectors]\)是支持向量的期望值。這個上界的產生是出于這樣的一個思想：僅僅支持向量的變化才會引起超平面的變動，致使在最壞的情況下所有的支持向量都被誤分類。但是據[10]指出：很多情形下即使支持向量數目減少了，實際的誤差也還是會增大。所以，該上界不能提供準確的錯誤信息。即便如此，我們卻可以根據這個現象得出一個結論： 支持向量的數目不能作為衡量SVM泛化性能的指標 。?

那么在實際應用中，我們又如何選擇合適的模型？模型選擇[6]方法很多，大家最為熟悉的交叉驗證(Cross Validation)就是其中之一。下面只簡要介紹結構風險最小化的內容。

Structure Risk Minimization

在機器學習中，我們必須根據有限的訓練數據選擇一個泛化模型(假設函數)來完成后續的預測任務，而選出來的這個泛化模型很有可能存在過擬合問題，即在訓練數據上能很好擬合數據，但是在新數據上的預測結果卻非常糟糕。結構風險定義為經驗風險與VC置信度之和，構成了泛化誤差的上界。結構風險最小化(Structure Risk Minimization, SRM)[7]通過在模型復雜度和訓練數據上的擬合程度之間尋找一個平衡點，以解決過擬合問題，這也是VC維的一個應用場合。 結合圖7，我們將結構風險最小化的步驟簡要描述為如下四步:

1. 根據先驗知識選擇一種類型的假設函數形成假設集合\(\mathcal{H}\)，比如\(n\)次多項式或者有\(n\)個隱含結點的三層神經網絡；
2. 根據模型復雜度(VC維)遞增的順序將\(\mathcal{H}\)劃分成若干逐層嵌套的假設集合\(\mathcal{H}_1\subseteq\mathcal{H}_2\subseteq\mathcal{H}_3\subseteq\cdots\subseteq\mathcal{H}\)，比如\(\mathcal{H}_t\)可以是對應\(t\)次多項式的假設函數集合；
3. 依次在每個\(\mathcal{H}_t\)上以經驗風險最小化為原則選擇假設函數\(\hat{h}_t\in\mathcal{H}_t\);
4. 選擇使泛化誤差上界(經驗風險+VC置信度)最小的模型為最優模型，在上界相同的情形下優先選擇復雜度最低的模型。

References

[1] Chernoff bound. http://en.wikipedia.org/wiki/Chernoff_bound .

[2] Empirical risk minimization. http://en.wikipedia.org/wiki/Empirical_risk_minimization .

[3] Hoeffding’s inequality. http://en.wikipedia.org/wiki/Hoeffding’s_inequality .

[4] Jensen’s inequality. http://en.wikipedia.org/wiki/Jensen’s_inequality .

[5] Markov’s inequality. http://en.wikipedia.org/wiki/Markov_inequality .

[6] Model selection. http://en.wikipedia.org/wiki/Model_selection .

[7] Structural risk minimization. http://www.svms.org/srm/ .

[8] Union bound. http://en.wikipedia.org/wiki/Boole’s_inequality .

[9] VC dimension. http://www.svms.org/vc-dimension/ .

[10] Christopher JC Burges. A tutorial on support vector machines for pattern recognition. Data mining and knowledge discovery, 2(2):121–167, 1998.

[11] Vapnik-chervonenkis learning theory. http://cmp.felk.cvut.cz/~hlavac/TeachPresEn/31PattRecog/27VapnikChervonenkis.pdf

Learning Theory